Steve loves squares and rectangles, and eating things like lava chicken. Today, he has been given a rectangular cake made up of a grid of square ~1 \times 1~ blocks which may either contain icing or a berry.

Steve doesn't like eating his daily intake of fruit, so he wants to cut the cake into rectangles (without cutting through any of the blocks) so that each slice has exactly one berry.

But he is having trouble — maybe it is impossible, or there is only one way to do it? Can you help him determine if it is possible to cut the cake as requested, and if possible, whether the cutting is unique?

Input

The first line of input contains two integers, ~h~ and ~w~, representing the height of the cake and the width of the cake, respectively, and satisfying ~1 \le h,w \le 1000~.

The following ~h~ lines of input contain ~w~ characters each, representing the toppings of the blocks in each row of the cake. A . represents icing and a # represents a berry.

There is guaranteed to be at least one berry.

Output

Output a single line:

• if there is no possible cutting satisfying Steve's requirements, output no cuttings;
• if there is a single possible cutting, output unique cutting; and
• if there are at least two possible cuttings, output multiple cuttings.

Note that non-identical rotations and reflections are considered to be distinct cuttings (e.g., see the explanation for example input/output 2).

Examples

Input 1

2 3
.##
...

Output 1

unique cutting

Explanation

In Sample ~1~, the only way to cut the cake into rectangles each containing a single berry is a ~2 \times 2~ rectangle on the left and a ~2 \times 1~ rectangle on the right, as in:

Input 2

3 3
.#.
###
.#.

Output 2

multiple cuttings

Explanation

In Sample ~2~, there are multiple ways to cut the cake. For example, the following three cuttings are all considered to be different (even though the third is a rotation of the second):

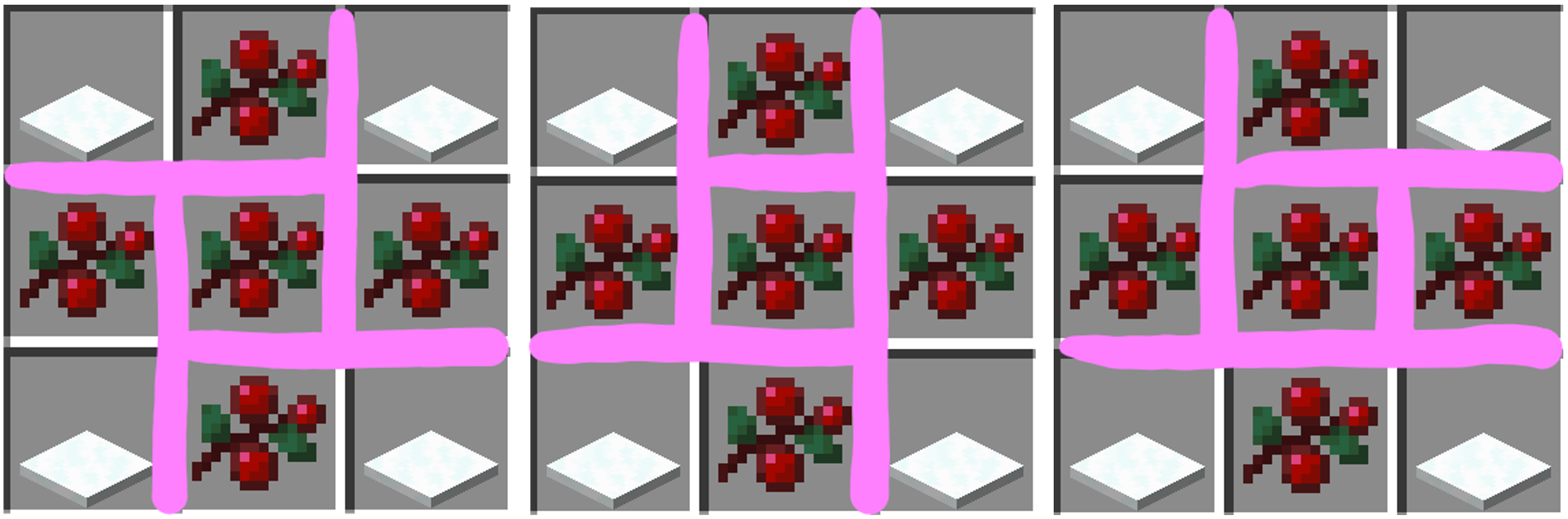
Sample 3

14 14
..............
..............
....#.....##..
..........##..
..............
.#....##......
.....####.....
.....####..#..
......##......
...#..........
.........##...
.........##...
...#..........
..............

Output 3

multiple cuttings